We prove here that the cosine function cos(-x)=cos x is even using the unit circle.

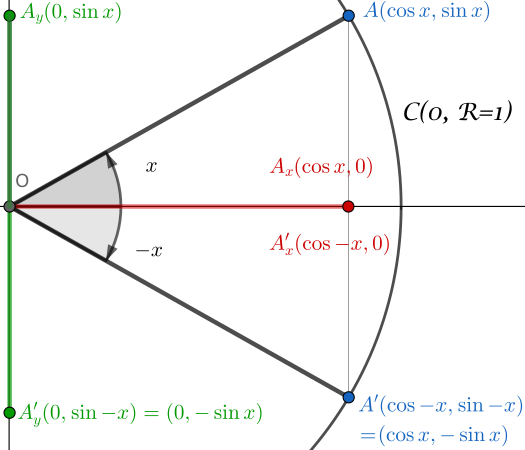
We start with the following configuration:

  • unit circle $\mathcal{C}(O,R=1)$
  • definition of the angle $x$
  • definition of the angle $-x$

Now consider the triangles: $(OA_xA)$ and $(OA’_xA’)$.

Proof that cosine is an even function cos(-x) = cos (x)

Take the definition of the cosines of the angles $x$ and $-x$.

In the triangle $(OA_xA)$ :

\[\cos x=\frac{\textrm{adjacent}}{\textrm{hypotenuse}}=\frac{|OA_x|}{R}=\frac{|OA_x|}{1}=|OA_x|\]

In the triangle $(OA’_xA’)$:

\[\cos (-x)=\frac{\textrm{adjacent}}{\textrm{hypotenuse}}=\frac{|OA'_x|}{R}=\frac{|OA'_x|}{1}=|OA'_x|\]

By construction: $\vert OA_x\vert = \vert OA’_x\vert $, then we have

\[\forall x\in \mathbb{R},\quad: \cos (-x)=\cos x\]