Dimostreremo che per qualsiasi angolo a, b, la formula di addizione in trigonometria cos (a+b)=cos a cos b - sin a sin b

Consideriamo un sistema di riferimento ortogonale $(O ; \vec{i}, \vec{j})$, $a$ e $b$ due numeri reali definiti come segue:

\[\begin{aligned} a&=(\vec{i}, \overrightarrow{O A}) \\ b&=(\overrightarrow{O A}, \overrightarrow{O B}) \end{aligned}\]

Dove $A$ e $B$ sono i punti definiti sul cerchio trigonometrico relativi agli angoli $a$ e $b$.

Allora abbiamo:

\[a+\frac{\pi}{2}=\left(\vec{i}, \overrightarrow{O A^{\prime}}\right)\]

Dove $A^{\prime}$ è il punto definito sul cerchio trigonometrico relativamente all’angolo $\displaystyle a+\frac{\pi}{2}$ con $\left(\overrightarrow{O A}, \overrightarrow{O A^{\prime}}\right)=\displaystyle\frac{\pi}{2}$.

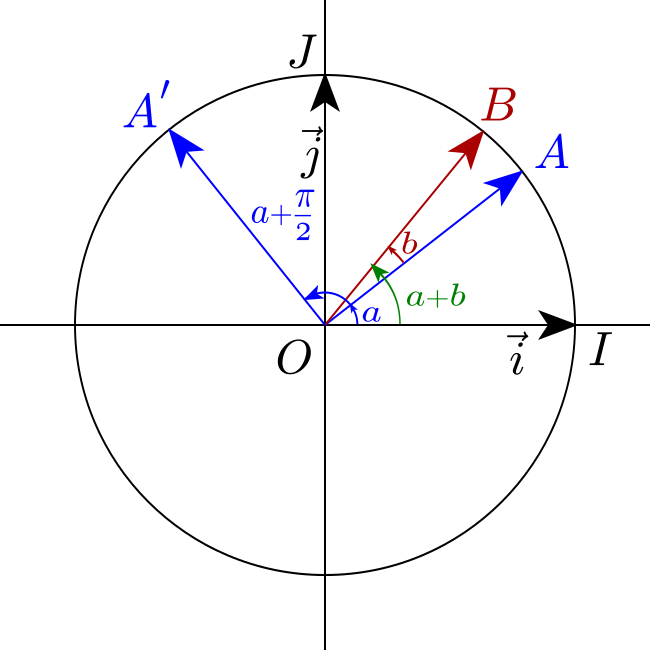
Per definizione, $\overrightarrow{O A}$ è definito come:

\[\overrightarrow{O A}=\cos a \times \vec{i} + \sin a \times \vec{j}\]

$\overrightarrow{O A^{\prime}}$ è definito come:

\[\overrightarrow{O A^{\prime}}=\cos \left(a+\frac{\pi}{2}\right) \times\vec{i}+\sin \left(a+\frac{\pi}{2}\right) \times\vec{j} = -\sin a \times \vec{i} + \cos a \times \vec{j}\]

$\overrightarrow{O B}$ è definito da:

\[\overrightarrow{O B}=\cos (a+b) \times\vec{i}+\sin (a+b) \times \vec{j}\]

Consideriamo il sistema di riferimento ortogonale $\left(O ; \overrightarrow{OA}, \overrightarrow{O A^{\prime}}\right)$. Il vettore $\overrightarrow{O B}$ in questo sistema di riferimento è definito come:

\[\begin{aligned} \overrightarrow{O B} &=\cos b \times \overrightarrow{OA} + \sin b \times \overrightarrow{O A^{\prime}} \\ &=\cos b \times (\cos a \times \vec{i} + \sin a \times\vec{j}) + \sin b \times (-\sin a \times\vec{i} + \cos a \times\vec{j}) \\ &=(\cos a \times \cos b-\sin a \times \sin b) \times \vec{i}+(\sin a \times \cos b+\cos a \times \sin b) \times\vec{j} \end{aligned}\]

Ma abbiamo dimostrato che

\[\overrightarrow{O B}=\cos (a+b) \times\vec{i}+\sin (a+b) \times\vec{j}\]

Otteniamo quindi per identificazione:

\[\begin{aligned} \cos (a+b)&=\cos a \times \cos b-\sin a \times \sin b \\ \sin (a+b)&=\sin a \times \cos b+\cos a \times \sin b \end{aligned}\]

Abbiamo così dimostrato: \(\forall a,b \in \mathbb{R}, \quad \cos (a+b)=\cos a \cos b-\sin a \sin b\)