Vamos a demostrar que para cualquier ángulo a, b, la fórmula de adición en trigonometría cos (a+b)=cos a cos b - sen a sen b

Consideremos un sistema de referencia ortogonal $(O ; \vec{i}, \vec{j})$, $a$ y $b$ dos números reales definidos de la siguiente manera:

\[\begin{aligned} a&=(\vec{i}, \overrightarrow{O A}) \\ b&=(\overrightarrow{O A}, \overrightarrow{O B}) \end{aligned}\]

Donde $A$ y $B$ son los puntos definidos en el círculo trigonométrico en relación con los ángulos $a$ y $b$.

Entonces tenemos:

\[a+\frac{\pi}{2}=\left(\vec{i}, \overrightarrow{O A^{\prime}}\right)\]

Donde $A^{\prime}$ es el punto definido en el círculo trigonométrico en relación con el ángulo $\displaystyle a+\frac{\pi}{2}$ con $\left(\overrightarrow{O A}, \overrightarrow{O A^{\prime}}\right)=\displaystyle\frac{\pi}{2}$.

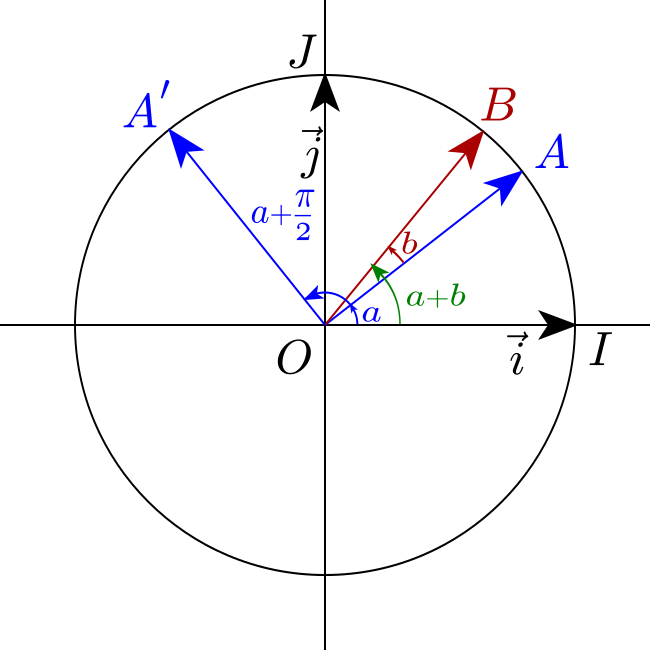
Por definición, $\overrightarrow{O A}$ se define como:

\[\overrightarrow{O A}=\cos a \times \vec{i} + \operatorname{sen} a \times \vec{j}\]

$\overrightarrow{O A^{\prime}}$ se define como:

\[\overrightarrow{O A^{\prime}}=\cos \left(a+\frac{\pi}{2}\right) \times\vec{i}+\operatorname{sen} \left(a+\frac{\pi}{2}\right) \times\vec{j} = -\operatorname{sen} a \times \vec{i} + \cos a \times \vec{j}\]

$\overrightarrow{O B}$ se define como:

\[\overrightarrow{O B}=\cos (a+b) \times\vec{i}+\operatorname{sen} (a+b) \times \vec{j}\]

Consideremos el sistema de referencia ortogonal $\left(O ; \overrightarrow{OA}, \overrightarrow{O A^{\prime}}\right)$. El vector $\overrightarrow{O B}$ en este sistema de referencia se define como:

\[\begin{aligned} \overrightarrow{O B} &=\cos b \times \overrightarrow{OA} + \operatorname{sen} b \times \overrightarrow{O A^{\prime}} \\ &=\cos b \times (\cos a \times \vec{i} + \operatorname{sen} a \times\vec{j}) + \operatorname{sen} b \times (-\operatorname{sen} a \times\vec{i} + \cos a \times\vec{j}) \\ &=(\cos a \times \cos b-\operatorname{sen} a \times \operatorname{sen} b) \times \vec{i}+(\operatorname{sen} a \times \cos b+\cos a \times \operatorname{sen} b) \times\vec{j} \end{aligned}\]

Pero hemos demostrado que

\[\overrightarrow{O B}=\cos (a+b) \times\vec{i}+\operatorname{sen} (a+b) \times\vec{j}\]

Obtenemos entonces por identificación:

\[\begin{aligned} \cos (a+b)&=\cos a \times \cos b-\operatorname{sen} a \times \operatorname{sen} b \\ \operatorname{sen} (a+b)&=\operatorname{sen} a \times \cos b+\cos a \times \operatorname{sen} b \end{aligned}\]

Hemos demostrado así que para cualquier ángulo $a$, $b$:

\[\cos (a+b)=\cos a \cos b-\operatorname{sen} a \operatorname{sen} b\]