Chebyshev polynomials
Chebyshev polynomials are a useful and important tool in the field of interpolation. Indeed, in order to minimize the error in Lagrange interpolation, the roots of Chebychev polynomials are definitely the best suited points of interpolation. Other names: Chebysheff, Chebyshov, Tschebyscheff, Tschebycheff
Definition
Let $n\in \mathbf{N}$. The Chebyshev polynomial of degree $n$ is the map defined as follows:
\[T_n:[-1,1] \rightarrow \mathbf{R},\quad x \longmapsto \cos (n\operatorname{Arccos} x)\]Explicit computation of Chebyshev Polynomials
Let $x\in [-1,1]$ and $\alpha=\operatorname{Arccos} x$.
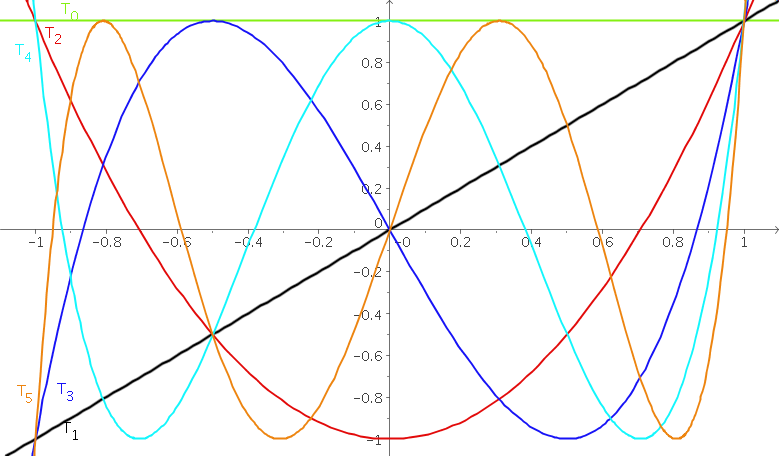
\[\begin{array}{ccl} T_n(x)&=&\Re((\cos n\alpha +i\sin n\alpha))\\ &=&\Re((\cos \alpha +i\sin \alpha)^n)\\ &=&\Re((\cos \operatorname{Arccos} x +i\sin \operatorname{Arccos} x)^n)\\ &=&\Re(( x +i\sqrt{1-x^2})^n)\\ &=&\Re(\displaystyle\sum_{k=0}^n C_{n}^{k}x^{n-k} i^{k}(\sqrt{1-x^2})^k)\\ &=&\displaystyle\sum_{k=0}^{E[n/2]} C_{n}^{2k}x^{n-2k} (i)^{2k}(1-x^2)^k\\ &=&\displaystyle\sum_{k=0}^{E[n/2]} C_{n}^{2k}x^{n-2k}(x^2-1)^k \end{array}\]where $E$ is the floor function and $\Re$ is the real part. The following table gives the first Chebyshev polynomials:
| $n$ | $T_n$ |
| 0 | 1 |
| 1 | $x$ |
| 2 | $2x^2-1$ |
| 3 | $4x^3-3x$ |
| 4 | $8x^4-8x^2+1$ |
| 5 | $16x^5-20x^3+5x$ |
Recurrence relation between Chebyshev polynomials
Proposition. $T_0(x)=1$, $T_1(x)=x$ and for any number $n\in\mathbf{N}$
\[T_{n+2}(x)=2xT_{n+1}(x)-T_n(x)\]Proof. Let $x\in[-1,1]$ and $\alpha=\operatorname{Arccos} x$. By means of trigonometry formulae, we have the following two equalities:
\(\cos (n+2)\alpha = \cos (n+1)\alpha \cdot \cos \alpha - \sin (n+1)\alpha \cdot \sin \alpha\) \(\cos n\alpha = \cos (n+1)\alpha \cdot \cos \alpha + \sin (n+1)\alpha \cdot \sin \alpha\)
Adding these two equalities, one obtains:
\[\cos (n+2)\alpha + \cos n\alpha = 2\cos (n+1)\alpha \cdot \cos \alpha\]Therefore, for any $x$ in $[-1,1]$:
\[T_{n+2}(x)+T_n(x)=2xT_{n+1}(x)\]Proposition. The coefficient of the $n^{th}$-degree term of $T_n$ is $2^{n-1}$.
Proof. We shall proceed by induction. The coefficient of $T_1$ is $1=2^{1-1=0}$. Assume that the coefficient of the $n^{th}$-degree term of $T_n$ is $2^{n-1}$. Then, given the previous recurrence relation, one can see that the coefficient of the $n+1^{th}$-degree term is twice that of $T_n$ ($2x\times\ldots)$. Thus, $2\times 2^{n-1}=2^{n}$.
Orthogonality of Chebyshev polynomials
Chebyshev polynomials are pairwise $w$-orthogonal; that is, they are orthogonal with regard to a weighted function defined by:
\[w(x)=\frac{1}{\sqrt{1-x^2}}\]In particular:
\[\int_{-1}^{1}T_n(x)T_m(x)w(x)dx= \left\{\begin{array}{ccl} \displaystyle\pi &si& n=m=0\\ \displaystyle \frac{\pi}{2} &si& n=m\neq 0\\ \displaystyle 0 &si& n\neq m\\ \end{array} \right.\]Proof. To compute the previous integral, we use the following substitution: \(x=\cos \theta,\quad dx=-\sin\theta d\theta\)
We thus have:
\[\begin{array}{ccl} \displaystyle \int_{-1}^{1}T_n(x)T_m(x)w(x)dx&=& -\displaystyle \int_{\pi}^{0}\frac{\cos n\theta \cdot\cos m\theta \sin \theta}{|\sin \theta|}d\theta\\ &=& \displaystyle \int_{0}^{\pi}\cos n\theta \cdot\cos m\theta d\theta\\ &=&\displaystyle \frac{1}{2} \int_{0}^{\pi}\cos (n+m)\theta +\cos (n-m)\theta d\theta\\ \end{array}\]The conclusion is therefore obvious.
Roots of Chebyshev polynomials
Proposition. Let $n\in \mathbf{N}^{*}$. $T_n$ has {exactly} $n$ simple roots defined as follows:
\[x_k=\cos \left(\frac{2k+1}{2n}\pi\right),\quad k=0,1,\ldots,n-1.\]Proof. Let $n\in \mathbf{N}^{*}$ and $k=0,1,\ldots,n-1$:
\[\begin{array}{ccl} T_n(x_k)&=&\displaystyle\cos (n\operatorname{Arccos} x_k)\\ &=&\displaystyle\cos (n\operatorname{Arccos}\cos \left(\frac{2k+1}{2n}\pi\right) )\\ &=&\displaystyle\cos n\left(\frac{2k+1}{2n}\pi\right)\\ &=&\displaystyle\cos \left(\frac{2k+1}{2}\pi\right)\\ &=&0 \end{array}\]Since $T_n$ has degree $n$, the $(x_k)_{k=0,1,\ldots,n-1}$ are precisely the roots of $T_n$. They are simple roots since for all $k\neq k’$, we have $x_k\neq x_{k’}$
Extrema of Chebyshev polynomials
Proposition. Let $n\in \mathbf{N}^{*}$. $T_n$ has exactly $(n+1)$ extrema defined by:
\[x'_k=\cos \left(\frac{k\pi}{n}\right),\quad k=0,1,\ldots,n.\]Proof. Let $n\in \mathbf{N}^{*}$ and $k=0,1,\ldots,n$. The first derivative of $T_n$ is:
\[\forall x\in [-1,1],T'_n(x)=\frac{n}{\sqrt{1-x^2}}\sin (n\operatorname{Arccos} x)\]Therefore:
\[\begin{array}{ccl} T'_n(x'_k)&=&\displaystyle\frac{n}{\sqrt{1-(x'_k)^2}}\sin (n\operatorname{Arccos} x'_k)\\ &=&\displaystyle\frac{n}{\sqrt{1-\cos^2\left(\frac{k\pi}{n}\right)}}\sin (n\operatorname{Arccos} \cos \left(\frac{k\pi}{n}\right))\\ &=&\displaystyle\frac{n}{\sqrt{1-\cos^2\left(\frac{k\pi}{n}\right)}}\sin (k\pi)\\ &=&0 \end{array}\]Proposition.
\[T_n(x'_k)=(-1)^k,\quad k=0,1,\ldots,n.\]Proof.
\[\begin{array}{ccl} T_n(x'_k)&=&\displaystyle\cos (n\operatorname{Arccos} x'_k)\\ &=&\displaystyle\cos (n\operatorname{Arccos} \cos \left(\frac{k\pi}{n}\right))\\ &=&\displaystyle\cos (n\frac{k\pi}{n})\\ &=&\displaystyle\cos (k\pi)\\ &=&(-1)^k \end{array}\]The maximum reached by Chebyshev polynomials
A forthwith consequence of the previous propositions is that:
\[\max_{[-1,1]} |T_n(x)|=1\]Best choice of points of interpolation of Lagrange polynomial
We have seen that if $f\in \mathcal{C}^{n+1}([a,b])$ and $x\in[a,b]$, then:
\[\forall x\in [a,b],\quad |f(x)-P_n(x)|\leq \displaystyle\frac{\displaystyle|(x-x_0)(x-x_1)\ldots(x-x_n)|}{(n+1)!}\sup_{x\in[a,b]}|f^{n+1} (x)|\]The aim is to determine the points of interpolation $(x_k)_{k=0,1,\ldots,n}$ such that
\[\sup_{x\in[a,b]}|(x-x_0)(x-x_1)\ldots(x-x_n)|\leq \sup_{x\in[a,b]}|Q(x)|\]for all $n+1^{nth}$-degree monic polynomials $Q$. Via an affine substitution, the equivalent problem is:
\[\sup_{x\in[-1,1]}|(x-x_0)(x-x_1)\ldots(x-x_n)|\leq \sup_{x\in[-1,1]}|Q(x)|\]We shall prove that the points of interpolation that verify this property are precisely te roots of the Chebyshev polynomial $T_{n+1}$.
Theorem.
\[\sup_{x\in[-1,1]}|(x-x_0)(x-x_1)\ldots(x-x_n)|\leq \sup_{x\in[-1,1]}|Q(x)|\]where
\[x_k=\cos \left(\frac{2k+1}{2(n+1)}\pi\right),\quad k=0,1,\ldots,n.\]Proof.
Let
\[\bar{T}_{n+1}=\frac{1}{2^n}T_{n+1}\]be the monic Chebyshev polynomial associated to $T_{n+1}$.
The roots of $\bar{T}_{n+1}$ are those of $T_{n+1}$ and are defined by
\[x_k=\cos \left(\frac{2k+1}{2(n+1)}\pi\right),\quad k=0,1,\ldots,n.\]We have:
\[\bar{T}_{n+1}=(x-x_0)(x-x_1)\ldots(x-x_n)\]Additionally:
\[\begin{array}{ccl} \displaystyle \sup_{x\in[-1,1]}|(x-x_0)(x-x_1)\ldots(x-x_n)|&=&\displaystyle \sup_{x\in[-1,1]} |\bar{T}_{n+1}(x)|\\ &=&\displaystyle\frac{1}{2^n}\sup_{x\in[-1,1]} |T_{n+1}(x)|\\ &=&\displaystyle\frac{1}{2^n} \end{array}\]Since
\[\bar{T}_{n+1}(x'_k)=\frac{1}{2^n}T_{n+1}(x'_k)=\frac{(-1)^k}{2^n}.\]where
\[x'_k=\cos \left(\frac{k\pi}{(n+1)}\right),\quad k=0,1,\ldots,n+1.\]We thus have to show that:
\[\frac{1}{2^n}\leq \sup_{x\in[-1,1]}|Q(x)|\]We shall proceed by contradiction by assuming that:
\[\frac{1}{2^n} > \sup_{x\in[-1,1]}|Q(x)|.\]Since $Q$ and $\bar{T}_{n+1}$ are monic polynomials:
\[\deg (Q-\bar{T}_{n+1})=n.\]Also
\[\begin{array}{ccl} \forall k=0,1,\ldots,n+1,\quad (Q-\bar{T}_{n+1})(x'_k)&=&Q(x'_k)-\bar{T}_{n+1}(x'_k)\\ &=&\displaystyle Q(x'_k)-\frac{(-1)^k}{2^n} \end{array}\]If $k$ is an even number:
\[(Q-\bar{T}_{n+1})(x'_k)=\displaystyle Q(x'_k)-\frac{(-1)^k}{2^n}< \displaystyle\frac{1}{2^n}-\frac{1}{2^n}=0\]If $k$ is an odd number:
\[(Q-\bar{T}_{n+1})(x'_k)=\displaystyle Q(x'_k)-\frac{(-1)^k}{2^n}>\displaystyle-\frac{1}{2^n}-\frac{-1}{2^n}=0\]Finally:
\[(Q-\bar{T}_{n+1})(x'_k)(Q-\bar{T}_{n+1})(x'_{k+1})<0,\quad\forall k=0,1,\ldots,n\]This means that there are $(n+1)$ sign changes for the map $(Q-\bar{T}_{n+1})$.
Consequently $(Q-\bar{T}_{n+1})$ has $(n+1)$ roots.
But, $(Q-\bar{T}_{n+1})$ has degree $n$. Therefore:
\[Q-\bar{T}_{n+1}=0\] \[Q=\bar{T}_{n+1}\]Finally:
\[\sup_{x\in[-1,1]}|Q(x)|=\sup_{x\in[-1,1]}|\bar{T}_{n+1}(x)|=\frac{1}{2^n}.\]which contradicts our assumption.
We finally conclude that:
\[\begin{array}{ccl} \displaystyle\frac{1}{2^n}&=&\displaystyle\sup_{x\in[-1,1]}|\bar{T}_{n+1}(x)|\\ &=&\displaystyle\sup_{x\in[-1,1]}|(x-x_0)(x-x_1)\ldots(x-x_n)|\\ &\leq&\displaystyle \sup_{x\in[-1,1]}|Q(x)| \end{array}\]If you found this post or this website helpful and would like to support our work, please consider making a donation. Thank you!
Help Us