Les polynômes de Tchebychev constituent un outil important dans le domaine de l’interpolation: en effet, on démontre que pour minimiser l’erreur d’interpolation de Lagrange, les racines des polynômes de Tchebychev sont les candidats pour être les points d’interpolations.

Définition

Soit $n\in \mathbf{N}$. On appelle polynôme de Tchebychev de degré $n$, l’application définit comme suit:

\[T_n:[-1,1] \rightarrow \mathbf{R},\quad x \longmapsto \cos (n\operatorname{Arccos} x)\]

Calcul explicite des polynômes de Tchebychev

Soit $x\in [-1,1]$ et $\alpha=\operatorname{Arccos} x$.

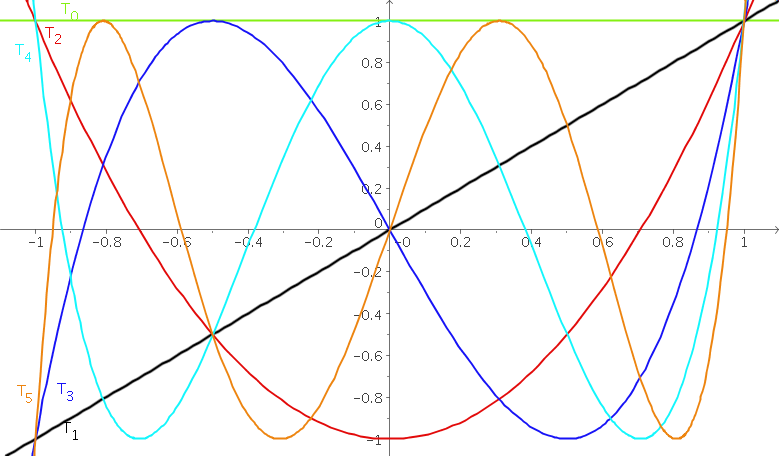
\[\begin{array}{ccl} T_n(x)&=&\Re((\cos n\alpha +i\sin n\alpha))\\ &=&\Re((\cos \alpha +i\sin \alpha)^n)\\ &=&\Re((\cos \operatorname{Arccos} x +i\sin \operatorname{Arccos} x)^n)\\ &=&\Re(( x +i\sqrt{1-x^2})^n)\\ &=&\Re(\displaystyle\sum_{k=0}^n C_{n}^{k}x^{n-k} i^{k}(\sqrt{1-x^2})^k)\\ &=&\displaystyle\sum_{k=0}^{E[n/2]} C_{n}^{2k}x^{n-2k} (i)^{2k}(1-x^2)^k\\ &=&\displaystyle\sum_{k=0}^{E[n/2]} C_{n}^{2k}x^{n-2k}(x^2-1)^k \end{array}\]

où $E$ désigne la partie entière et $\Re$ la partie réelle. Le tableau suivant donne les premiers polynômes de Tchebychev:

$n$ $T_n$
0 1
1 $x$
2 $2x^2-1$
3 $4x^3-3x$
4 $8x^4-8x^2+1$
5 $16x^5-20x^3+5x$

Relation de récurrence entre les polynômes de Tchebychev

Proposition.On a $T_0(x)=1$ et $T_1(x)=x$ et pour tout $n\in\mathbf{N}$

\[T_{n+2}(x)=2xT_{n+1}(x)-T_n(x)\]

Preuve. Soit $x\in[-1,1]$ et $\alpha=\operatorname{Arccos} x$. On a en utilisant les formules de trigonométrie classiques, on a les deux égalités suivantes:

\[\cos (n+2)\alpha = \cos (n+1)\alpha \cdot \cos \alpha - \sin (n+1)\alpha \cdot \sin \alpha\] \[\cos n\alpha = \cos (n+1)\alpha \cdot \cos \alpha + \sin (n+1)\alpha \cdot \sin \alpha\]

En sommant ces deux égalités, on obtient:

\[\cos (n+2)\alpha + \cos n\alpha = 2\cos (n+1)\alpha \cdot \cos \alpha\]

On a alors que pour tout $x$ dans $[-1,1]$:

\[T_{n+2}(x)+T_n(x)=2xT_{n+1}(x)\]

Proposition.Le coefficient du terme de degré $n$ de $T_n$ est $2^{n-1}$.

Preuve. On procède par récurrence: le coefficient de $T_1$ est $1=2^{1-1=0}$. Supposons que le coefficient du terme de degré $n$ de $T_n$ soit $2^{n-1}$, alors on voit d’apres la relation de récurrence précédente que le coefficient du terme de degré $(n+1)$ est deux fois celui de $T_n$ ($2x\times\ldots)$ donc $2\times 2^{n-1}=2^{n}$.

Orthogonalité des polynômes de Tchebychev

Les polynômes de Tchebychev sont $w$-orthogonaux, c’est à dire orthogonaux relativement à la fonction poids définie par:

\[w(x)=\frac{1}{\sqrt{1-x^2}}\]

En l’occurence, on a:

\[\int_{-1}^{1}T_n(x)T_m(x)w(x)dx= \left\{\begin{array}{ccl} \displaystyle\pi &si& n=m=0\\ \displaystyle \frac{\pi}{2} &si& n=m\neq 0\\ \displaystyle 0 &si& n\neq m\\ \end{array} \right.\]

Preuve.Pour calculer l’intégrale précédente, on fait le changement de variable:

\[x=\cos \theta,\quad dx=-\sin\theta d\theta\]

On a alors:

\[\begin{array}{ccl} \displaystyle \int_{-1}^{1}T_n(x)T_m(x)w(x)dx&=& - \displaystyle \int_{\pi}^{0}\frac{\cos n\theta \cdot\cos m\theta \sin \theta}{|\sin \theta|}d\theta\\ &=& \displaystyle \int_{0}^{\pi}\cos n\theta \cdot\cos m\theta d\theta\\ &=&\displaystyle \frac{1}{2} \int_{0}^{\pi}\cos (n+m)\theta +\cos (n-m)\theta d\theta\\ \end{array}\]

Il est alors facile de conclure.

Racines des polynômes de Tchebychev

Proposition. Soit $n\in \mathbf{N}^{*}$. $T_n$ admet exactement $n$ racines simples définies par:

\[x_k=\cos \left(\frac{2k+1}{2n}\pi\right),\quad k=0,1,\ldots,n-1.\]

Preuve. Soit $n\in \mathbf{N}^{*}$ et $k=0,1,\ldots,n-1$:

\[\begin{array}{ccl} T_n(x_k)&=&\displaystyle\cos (n\operatorname{Arccos} x_k)\\ &=&\displaystyle\cos (n\operatorname{Arccos}\cos \left(\frac{2k+1}{2n}\pi\right) )\\ &=&\displaystyle\cos n\left(\frac{2k+1}{2n}\pi\right)\\ &=&\displaystyle\cos \left(\frac{2k+1}{2}\pi\right)\\ &=&0 \end{array}\]

$T_n$ étant de degré $n$, les $(x_k)_{k=0,1,\ldots,n-1}$ sont exactement les zéros de $T_n$. Elles sont simples puisque pour tout $k\neq k’$, on a $x_k\neq x_{k’}$

Extrema des polynômes de Tchebychev

Proposition. Soit $n\in \mathbf{N}^{*}$. $T_n$ admet exactement $(n+1)$ extrema définis par:

\[x'_k=\cos \left(\frac{k\pi}{n}\right),\quad k=0,1,\ldots,n.\]

Preuve. Soit $n\in \mathbf{N}^{*}$ et $k=0,1,\ldots,n$. La dérivée de $T_n$ est définie:

\[\forall x\in [-1,1],T'_n(x)=\frac{n}{\sqrt{1-x^2}}\sin (n\operatorname{Arccos} x)\]

On a alors:

\[\begin{array}{ccl} T'_n(x'_k)&=&\displaystyle\frac{n}{\sqrt{1-(x'_k)^2}}\sin (n\operatorname{Arccos} x'_k)\\ &=&\displaystyle\frac{n}{\sqrt{1-\cos^2\left(\frac{k\pi}{n}\right)}}\sin (n\operatorname{Arccos} \cos \left(\frac{k\pi}{n}\right))\\ &=&\displaystyle\frac{n}{\sqrt{1-\cos^2\left(\frac{k\pi}{n}\right)}}\sin (k\pi)\\ &=&0 \end{array}\]

Proposition.

\[T_n(x'_k)=(-1)^k,\quad k=0,1,\ldots,n.\]

Preuve.

\[\begin{array}{ccl} T_n(x'_k)&=&\displaystyle\cos (n\operatorname{Arccos} x'_k)\\ &=&\displaystyle\cos (n\operatorname{Arccos} \cos \left(\frac{k\pi}{n}\right))\\ &=&\displaystyle\cos (n\frac{k\pi}{n})\\ &=&\displaystyle\cos (k\pi)\\ &=&(-1)^k \end{array}\]

Maximum atteint par les polynômes de Tchebychev

Une conséquence immédiate des propositions suivantes est que:

\[\max_{[-1,1]} |T_n(x)|=1\]

Meilleur choix des points d’interpolation du polynôme de Lagrange

Nous avons vu que si $f\in \mathcal{C}^{n+1}([a,b])$ et $x\in[a,b]$, on a:

\[\forall x\in [a,b],\quad |f(x)-P_n(x)|\leq \displaystyle\frac{\displaystyle|(x-x_0)(x-x_1)\ldots(x-x_n)|}{(n+1)!}\sup_{x\in[a,b]}|f^{n+1} (x)|\]

L’objectif est de déterminer les points d’interpolation $(x_k)_{k=0,1,\ldots,n}$ de telle manière que

\[\sup_{x\in[a,b]}|(x-x_0)(x-x_1)\ldots(x-x_n)|\leq \sup_{x\in[a,b]}|Q(x)|\]

pour tout polynôme $Q$ normalisé de degré $(n+1)$. Par un changement de variable affine, il est équivalent de résoudre le problème suivant:

\[\sup_{x\in[-1,1]}|(x-x_0)(x-x_1)\ldots(x-x_n)|\leq \sup_{x\in[-1,1]}|Q(x)|\]

Nous allons montrer que les point d’interpolation qui vérifient cette propriété sont exactement les racines du polynôme de Tchebychev $T_{n+1}$.

Théorème.

\[\sup_{x\in[-1,1]}|(x-x_0)(x-x_1)\ldots(x-x_n)|\leq \sup_{x\in[-1,1]}|Q(x)|\]

avec

\[x_k=\cos \left(\frac{2k+1}{2(n+1)}\pi\right),\quad k=0,1,\ldots,n.\]

Preuve.

Soit $\bar{T}_{n+1}=\frac{1}{2^n}T_{n+1}$ le polynome de Tchebychev $T_{n+1}$ normalisé. Les racines de $\bar{T}_{n+1}$ sont donc celles de $T_{n+1}$ , elles sont définies par:

\[x_k=\cos \left(\frac{2k+1}{2(n+1)}\pi\right),\quad k=0,1,\ldots,n.\]

On a donc a fortiori

\[\bar{T}_{n+1}=(x-x_0)(x-x_1)\ldots(x-x_n)\]

Par ailleurs

\[\begin{array}{ccl} \displaystyle \sup_{x\in[-1,1]}|(x-x_0)(x-x_1)\ldots(x-x_n)|&=&\displaystyle \sup_{x\in[-1,1]} |\bar{T}_{n+1}(x)|\\ &=&\displaystyle\frac{1}{2^n}\sup_{x\in[-1,1]} |T_{n+1}(x)|\\ &=&\displaystyle\frac{1}{2^n} \end{array}\]

De plus

\[\bar{T}_{n+1}(x'_k)=\frac{1}{2^n}T_{n+1}(x'_k)=\frac{(-1)^k}{2^n}.\]

avec

\[x'_k=\cos \left(\frac{k\pi}{(n+1)}\right),\quad k=0,1,\ldots,n+1.\]

On doit donc montrer à présent que:

\[\frac{1}{2^n}\leq \sup_{x\in[-1,1]}|Q(x)|\]

nous allons raisonner par l’absurde en supposant que:

\[\frac{1}{2^n} > \sup_{x\in[-1,1]}|Q(x)|.\]

Puisque $Q$ et $\bar{T}_{n+1}$ sont normalisé, on a

\[\deg (Q-\bar{T}_{n+1})=n.\]

On a

\[\begin{array}{ccl} \forall k=0,1,\ldots,n+1,\quad (Q-\bar{T}_{n+1})(x'_k)&=&Q(x'_k)-\bar{T}_{n+1}(x'_k)\\ &=&\displaystyle Q(x'_k)-\frac{(-1)^k}{2^n} \end{array}\]

Si $k$ est pair:

\[(Q-\bar{T}_{n+1})(x'_k)=\displaystyle Q(x'_k)-\frac{(-1)^k}{2^n}< \displaystyle\frac{1}{2^n}-\frac{1}{2^n}=0\]

Si $k$ est impair:

\[(Q-\bar{T}_{n+1})(x'_k)=\displaystyle Q(x'_k)-\frac{(-1)^k}{2^n}>\displaystyle-\frac{1}{2^n}-\frac{-1}{2^n}=0\]

Au final:

\[(Q-\bar{T}_{n+1})(x'_k)(Q-\bar{T}_{n+1})(x'_{k+1})<0,\quad\forall k=0,1,\ldots,n,\quad\]

Cela veut donc dire qu’il y a $(n+1)$ changements de signe pour l’application $(Q-\bar{T}_{n+1})$, par suite $(Q-\bar{T}_{n+1})$ admet $(n+1)$ racines, or $(Q-\bar{T}_{n+1})$ est de degré $n$ donc:

\[Q-\bar{T}_{n+1}=0\] \[Q=\bar{T}_{n+1}\]

et donc

\[\sup_{x\in[-1,1]}|Q(x)|=\sup_{x\in[-1,1]}|\bar{T}_{n+1}(x)|=\frac{1}{2^n}.\]

ce qui contredit ce que l’on a supposé.

On conclut donc que:

\[\begin{array}{ccl} \displaystyle\frac{1}{2^n}&=&\displaystyle\sup_{x\in[-1,1]}|\bar{T}_{n+1}(x)|\\ &=&\displaystyle\sup_{x\in[-1,1]}|(x-x_0)(x-x_1)\ldots(x-x_n)|\\ &\leq&\displaystyle \sup_{x\in[-1,1]}|Q(x)| \end{array}\]