Come dimostrare che il limite di sin x / x = 1 quando x si avvicina a 0?

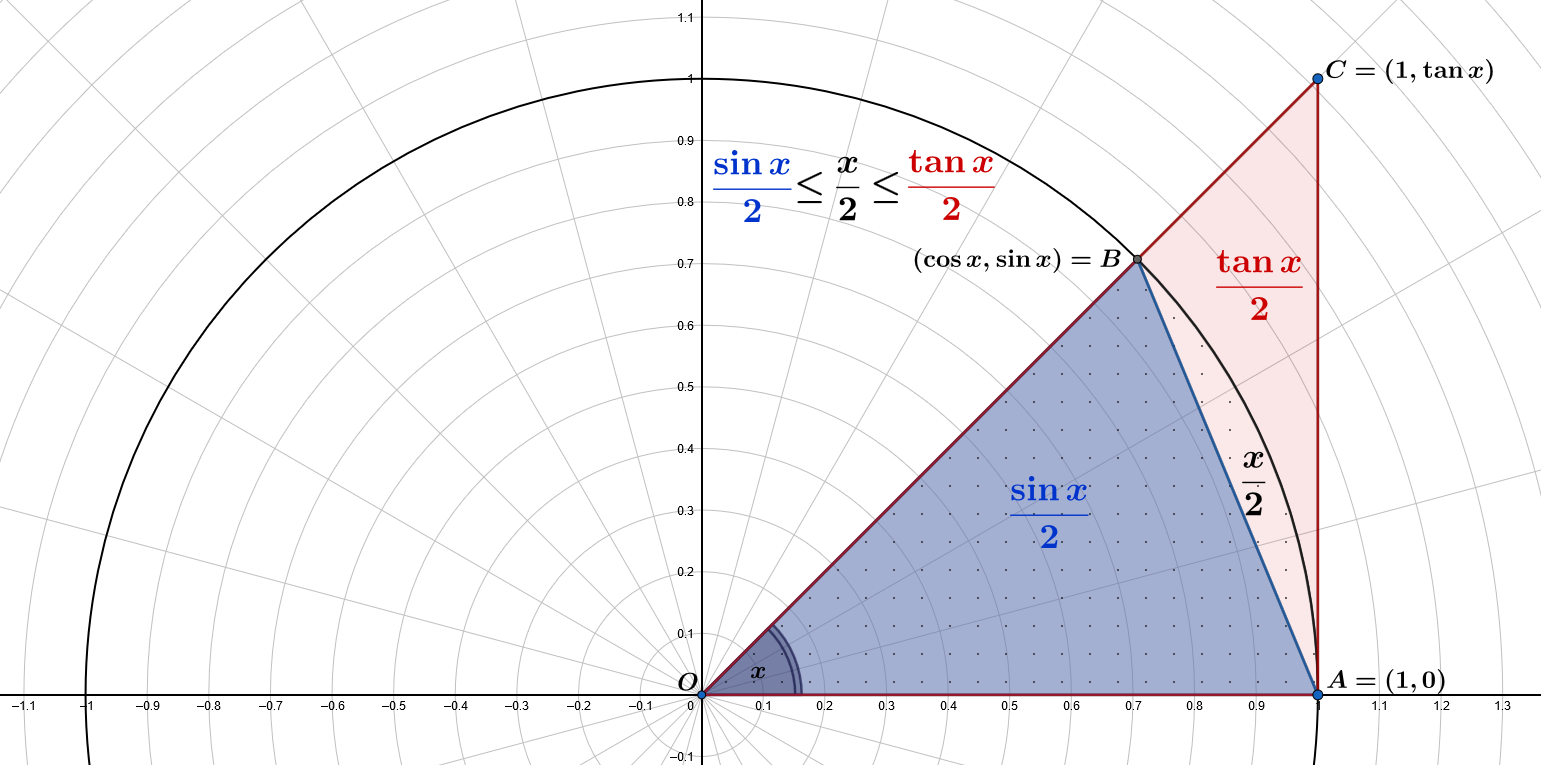
L’area del triangolo blu piccolo $\color{blue}{OAB}$ è $\displaystyle A(\color{blue}{OAB})=\frac{1\cdot\sin x}{2}=\color{blue}{\frac{\sin x}{2}}$

L’area del settore con i punti è $\displaystyle\pi\frac{x}{2\pi}=\frac{x}{2}$

L’area del grande triangolo rosso $\color{red}{OAC}$ è $\displaystyle A(\color{red}{OAC})=\frac{1\cdot\tan x}{2}=\color{red}{\frac{\tan x}{2}}$

Quindi, abbiamo $\displaystyle A(OAB) \leq \frac{x}{2} \leq A(OAC)$:

\[0\lt \sin x \leq x \leq \tan x, \quad\displaystyle\forall x \in ]0, \frac{\pi}{2}[\]

Poiché $0\lt \sin x$, si ha che \(\begin{aligned} \frac{\sin x}{\sin x} &\leq \frac{x}{\sin x} \leq \frac{\tan x}{\sin x}\\ 1&\leq \frac{x}{\sin x} \leq \frac{1}{\cos x}\\ \end{aligned}\)

Prendendo il reciproco:

\[\cos x \leq \frac{\sin x}{x} \leq 1\]

Dal momento che le funzioni $\displaystyle \cos x, \frac{\sin x}{x},1$ sono pari, concludiamo che:

\[\quad\cos x \leq \frac{\sin x}{x} \leq 1, \quad \displaystyle\forall x \in ]-\frac{\pi}{2}, 0[ \cup ]0, \frac{\pi}{2}[\]

Utilizzando il Teorema del confronto:

\[\lim _{x \rightarrow 0} \frac{\sin x}{x}= \lim _{x \rightarrow 0} \cos x=\lim _{x \rightarrow 0} 1 = 1\]

concludiamo che:

\[\lim _{x \rightarrow 0} \frac{\sin x}{x} = 1\]