सिन x / x की सीमा 0 के पास आने पर 1 होने का प्रमाण कैसे किया जाए?

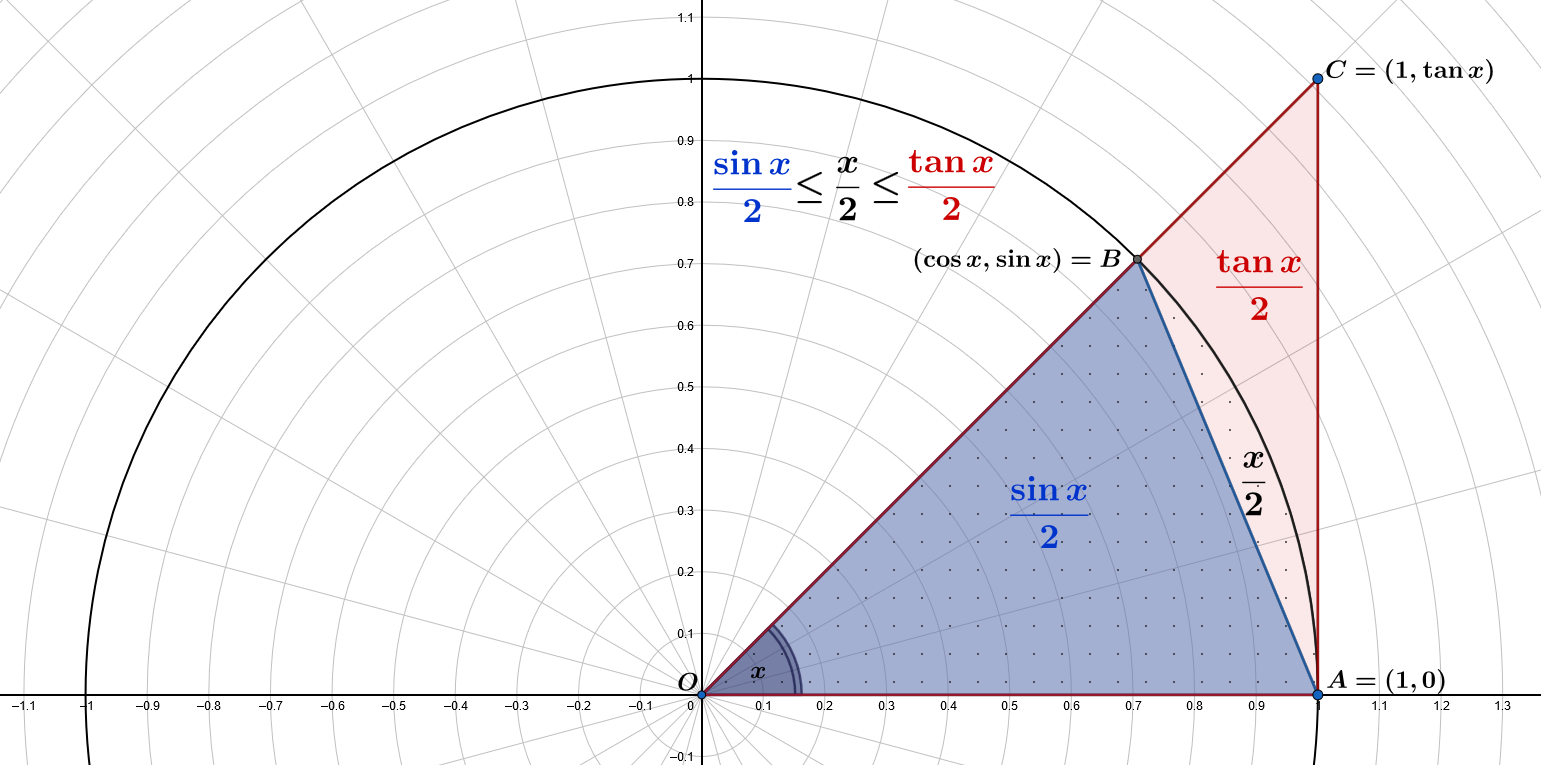
नीला छोटा त्रिभुज $\color{blue}{OAB}$ का क्षेत्रफल है $\displaystyle A(\color{blue}{OAB})=\frac{1\cdot\sin x}{2}=\color{blue}{\frac{\sin x}{2}}$

डॉट्स के साथ सेक्टर का क्षेत्रफल है $\displaystyle\pi\frac{x}{2\pi}=\frac{x}{2}$

लाल बड़ा त्रिभुज $\color{red}{OAC}$ का क्षेत्रफल है $\displaystyle A(\color{red}{OAC})=\frac{1\cdot\tan x}{2}=\color{red}{\frac{\tan x}{2}}$

इसके बाद, हमारे पास $\displaystyle A(OAB) \leq \frac{x}{2} \leq A(OAC)$ है:

\[0\lt \sin x \leq x \leq \tan x, \quad\displaystyle\forall x \in ]0, \frac{\pi}{2}[\]

क्योंकि $0\lt \sin x$ है, हमारे पास है \(\begin{aligned} \frac{\sin x}{\sin x} &\leq \frac{x}{\sin x} \leq \frac{\tan x}{\sin x}\\ 1&\leq \frac{x}{\sin x} \leq \frac{1}{\cos x}\\ \end{aligned}\)

पूरक लेने के बाद:

\[\cos x \leq \frac{\sin x}{x} \leq 1\]

क्योंकि $\displaystyle \cos x, \frac{\sin x}{x},1$ फ़ंक्शन सम, इसलिए हम इस निष्कर्षण पर पहुंचते हैं:

\[\quad\cos x \leq \frac{\sin x}{x} \leq 1, \quad \displaystyle\forall x \in ]-\frac{\pi}{2}, 0[ \cup ]0, \frac{\pi}{2}[\]

स्क्वीज थियोरी का उपयोग करके:

\[\lim _{x \rightarrow 0} \frac{\sin x}{x}= \lim _{x \rightarrow 0} \cos x=\lim _{x \rightarrow 0} 1 = 1\]

हम निष्कर्षण करते हैं कि:

\[\lim _{x \rightarrow 0} \frac{\sin x}{x} = 1\]