Preuve / démonstration de limite sin x / x = 1 quand x tend vers 0 ?

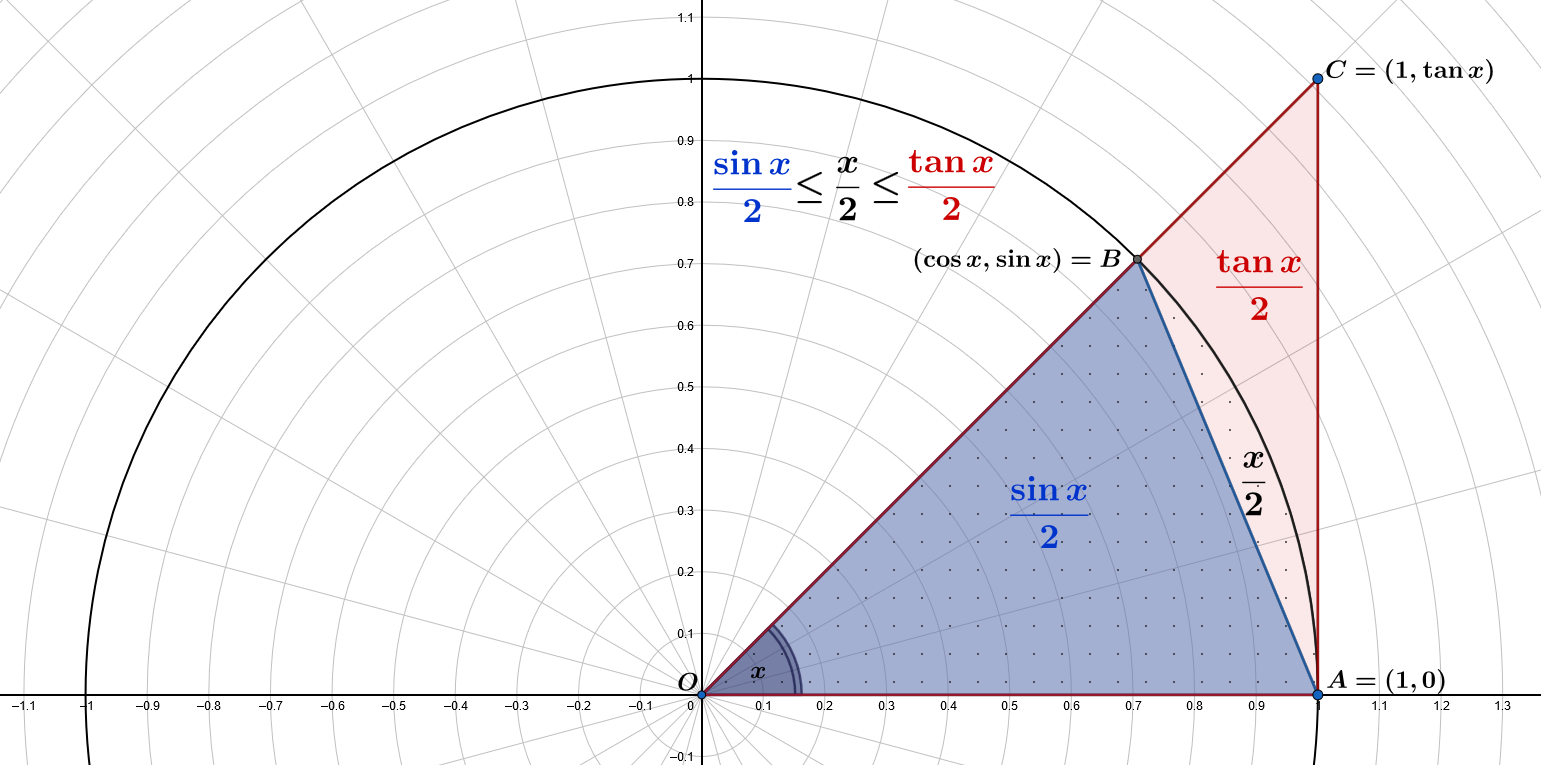
L’aire du triangle bleu $\color{blue}{OAB}$ est $\displaystyle A(\color{blue}{OAB})=\frac{1\cdot\sin x}{2}=\color{blue}{\frac{\sin x}{2}}$

L’aire de la la portion de cercle est $\displaystyle\pi\frac{x}{2\pi}=\frac{x}{2}$

L’aire du triangle rouge $\color{red}{OAC}$ est $\displaystyle A(\color{red}{OAC})=\frac{1\cdot\tan x}{2}=\color{red}{\frac{\tan x}{2}}$

On a alors $\displaystyle A(OAB) \leq \frac{x}{2} \leq A(OAC)$:

\[0\lt \sin x \leq x \leq \tan x, \quad\displaystyle\forall x \in ]0, \frac{\pi}{2}[\]

Puisque $0\lt \sin x$, on a \(\begin{aligned} \frac{\sin x}{\sin x} &\leq \frac{x}{\sin x} \leq \frac{\tan x}{\sin x}\\ 1&\leq \frac{x}{\sin x} \leq \frac{1}{\cos x}\\ \end{aligned}\)

En prenant l’inverse:

\[\cos x \leq \frac{\sin x}{x} \leq 1\]

$\displaystyle \cos x, \frac{\sin x}{x},1$ sont des fonctions paires, on conclut alors que:

\[\quad\cos x \leq \frac{\sin x}{x} \leq 1, \quad \displaystyle\forall x \in ]-\frac{\pi}{2}, 0[ \cup ]0, \frac{\pi}{2}[\]

En utilisant le théorème des gendarmes:

\[\lim _{x \rightarrow 0} \frac{\sin x}{x}= \lim _{x \rightarrow 0} \cos x=\lim _{x \rightarrow 0} 1 = 1\]

on a alors:

\[\lim _{x \rightarrow 0} \frac{\sin x}{x} = 1\]