Latex dérivée, limite, somme, produit et intégrale
Comment écrire en LateX les dérivées, limites, sommes, produits et intégrales ?
Dérivée en Latex ?
Sommes en Latex ?
Produits en Latex ?
Limites en Latex ?
Intégrales en Latex ?
Dérivée en Latex
Comment écrire des dérivées en Latex ?
| Définition | Code Latex | Résultat |
|---|---|---|
| Dérivée du premier ordre | f’(x) | \(\displaystyle f'(x)\) |
| Dérivée du second ordre | f’‘(x) | \(\displaystyle f''(x)\) |
| Dérivée d’ordre k | f^{(k)}(x) | \(\displaystyle f^{(k)}(x)\) |
| Dérivée partielle du premier ordre | \frac{\partial f}{\partial x} | \(\displaystyle \frac{\partial f}{\partial x}\) |
| Dérivée partielle du second ordre | \frac{\partial^2 f}{\partial x^2} | \(\displaystyle \frac{\partial^2 f}{\partial x^2}\) |
| Dérivée partielle d’ordre k | \frac{\partial^{k} f}{\partial x^k} | \(\displaystyle \frac{\partial^{k} f}{\partial x^k}\) |
Limite en Latex
Comment écrire des limites en Latex ?
| Définition | Code Latex | Résultat |
|---|---|---|
| Limite quand x tend vers plus l’infini | \lim_{x \to +\infty} f(x) | \(\displaystyle \lim_{x \to +\infty} f(x)\) |
| Limite quand x tend vers moins l’infini | \lim_{x \to -\infty} f(x) | \(\displaystyle \lim_{x \to -\infty} f(x)\) |
| Limite quand x tend vers $\alpha$ | \lim_{x \to \alpha} f(x) | \(\displaystyle \lim_{x \to \alpha} f(x)\) |
| Inf | \inf_{x > s}f(x) | \(\displaystyle \inf_{x > s}f(x)\) |
| Sup | \sup_{x \in \mathbb{R}}f(x) | \(\displaystyle \sup_{x \in \mathbb{R}}f(x)\) |
| Max | \max_{x \in [a,b]}f(x) | \(\displaystyle \max_{x \in [a,b]}f(x)\) |
| Min | \min_{x \in [\alpha,\beta]}f(x) | \(\displaystyle \min_{x \in [\alpha,\beta]}f(x)\) |
Somme en Latex
Comment écrire des sommes en Latex ?
| Définition | Code Latex | Résultat |
|---|---|---|
| Somme | \sum | \(\displaystyle \sum\) |
| Avec \limits | \sum\limits_{j=1}^k A_{\alpha_j} | \(\displaystyle \sum\limits_{j=1}^k A_{\alpha_j}\) |
| Sans \limits | \sum_{j=1}^k A_{\alpha_j} | \(\displaystyle \sum_{j=1}^k A_{\alpha_j}\) |
| Somme de 1 à n | \sum_{i=1}^n | \(\displaystyle \sum_{i=1}^n\) |
| Somme des n premiers entiers | \sum_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}{6} | \(\displaystyle \sum_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}{6}\) |
| Double somme | \sum^k_{i=1}\sum^l_{j=1}\,q_i q_j | \(\displaystyle \sum^k_{i=1}\sum^l_{j=1}\,q_i q_j\) |
Produit en Latex
Comment écrire des produits en Latex ?
| Définition | Code Latex | Résultat |
|---|---|---|
| Produit | \prod | \(\displaystyle \prod\) |
| Avec \limits | \prod\limits_{j=1}^k A_{\alpha_j} | \(\displaystyle \prod\limits_{j=1}^k A_{\alpha_j}\) |
| Sans \limits | \prod_{j=1}^k A_{\alpha_j} | \(\displaystyle \prod_{j=1}^k A_{\alpha_j}\) |
| Produit de 1 à n | \prod_{i=1}^n | \(\displaystyle \prod_{i=1}^n\) |
| Produit des n premiers entiers | \prod_{i=1}^n i | \(\displaystyle \prod_{i=1}^n i\) |
| Double produit | \prod^k_{i=1}\prod^l_{j=1}\,q_i q_j | \(\displaystyle \prod^k_{i=1}\prod^l_{j=1}\,q_i q_j\) |
Intégrale en Latex
| Définition | Code Latex | Résultat |
|---|---|---|
| Intégrale | \int | \(\displaystyle \int\) |
| Intégrale avec des limites | \int_{a}^b f(x)dx | \(\displaystyle \int_{a}^b f(x)dx\) |
| Double intégrale | \iint | \(\displaystyle \iint\) |
| Double intégrale avec des limites | \int_{a}^b\int_{c}^d f(x,y)dxdy | \(\displaystyle \int_{a}^b\int_{c}^d f(x,y)dxdy\) |
| Double intégrale avec des points de suspension | \idotsint | \(\displaystyle \idotsint\) |
| Triple intégrale | \iiint | \(\displaystyle \iiint\) |
| Quadruple intégrale | \iiiint | \(\displaystyle \iiiint\) |
| Intégrale de contour | \oint | \(\displaystyle \oint\) |
Intégrales de surface et de volume fermées en Latex
Pour définir de telles intégrales, vous devez utiliser le package wasysym
$$\oiint \oiiint$$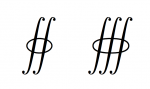
Si vous avez trouvé cet article ou ce site utile et souhaitez soutenir notre travail, veuillez envisager de faire un don. Merci !
Aidez-nousArticles dans la même rubrique
- Variance Symbol in LaTeX
- Union and Big Union Symbol in LaTeX
- Transpose Symbol in LaTeX
- Transformée de Laplace en LaTeX
- Texte au dessus d'une flèche en LaTeX
- Text above arrow in LaTeX
- Symbole "plus grand que ou similaire à" en LaTeX
- Symbole de Variance en LaTeX
- Symbole de transposée en LaTeX
- Symbole de "non équivalent à" en LaTeX
- Symbole d'union et de grande union en LaTeX
- Symbole d'intersection et de grande intersection en LaTeX
- Strikethrough - strike out text or formula in LaTeX
- Passer en mode mathématique en Latex: $, $$ et displaymath
- Partial Derivatives of Multivariable Functions in LaTeX
- Numéroter les équations en Latex: leqno et fleqn
- Not Equivalent Symbol in LaTeX
- Latex yen symbol
- Latex valeur absolue
- Latex tensor product
- Latex symbole sous-ensemble - inclusion
- Latex symbole racine carrée
- Latex symbole produit
- Latex symbole produit vectoriel
- Latex symbole pourcentage
- Latex symbole plus ou moins
- Latex symbole parallèle
- Latex symbole orthogonal - Latex symbole perpendiculaire
- Latex symbole norme pour un vecteur ou une somme
- Latex symbole n'existe pas
- Latex symbole n'est pas un sous-ensemble - non-inclus
- Latex symbole n'est pas parallèle
- Latex symbole n'appartient pas à
- Latex symbole multiplication
- Latex symbole loi normale
- Latex symbole infini
- Latex symbole il existe
- Latex symbole il existe un seul et unique
- Latex symbole euro
- Latex symbole Est proportionnel à
- Latex symbole espérance mathématiques
- Latex symbole équivalent / équivalence
- Latex symbole dual ou dague
- Latex symbole différent
- Latex symbole dérivée partielle
- Latex symbole degré
- Latex symbole de la moyenne
- Latex symbole de la constante de Planck h
- Latex symbole congruent
- LaTeX symbole complément
- Latex symbole chapeau
- Latex symbole approximativement
- Latex symbole appartient à
- Latex symbol there exists one and only one
- Latex symbol Planck constant h
- LaTex symbol partial derivative
- Latex symbol not in
- Latex symbol not exists
- Latex symbol not equal
- Latex symbol norm for vector and sum
- Latex symbol multiply
- LaTeX symbol Is proportional to
- Latex symbol if and only if / equivalence
- Latex symbol for all x
- Latex symbol exists
- Latex symbol different
- Latex symbol checkmark
- LaTeX symbol characteristic function
- Latex symbol belongs to
- Latex symbol average
- Latex symbol approximately
- Latex subset symbol
- Latex square root symbol
- Latex real part symbol
- Latex real numbers
- Latex rational numbers
- Latex quaternion numbers
- Latex produit tensoriel
- Latex product symbol
- Latex pour tout x
- Latex points de suspension: \ldots,\cdots,\vdots et \ddots
- Latex plus or minus symbol
- Latex piecewise function
- Latex partie réelle
- Latex partie imaginaire
- Latex parallel symbol
- Latex overset and underset
- Latex orthogonal symbol - Latex perpendicular symbol
- Latex numbering equations
- Latex not subset symbol
- Latex not parallel symbol
- Latex normal distribution symbol
- Latex natural numbers
- Latex k parmi n - coefficient binomial
- Latex jacobian symbol
- Latex infinity symbol
- Latex indicator function
- Latex imaginary part symbol
- Latex how to write underscore
- Latex how to write text in math mode
- Latex how to write percent
- Latex how to write bar
- Latex how to write a fraction
- Latex how to insert a blank or empty page with or without numbering \thispagestyle,\newpage,\usepackage{afterpage}
- Latex how to hide page number
- Latex horizontal space: qquad,hspace, thinspace,enspace
- Latex hat symbol - wide hat symbol
- Latex gradient symbol
- Latex fonction plancher - Latex partie entière inférieure
- Latex fonction plafond - Latex partie entière supérieure
- Latex fonction indicatrice
- Latex floor function
- Latex flèche
- Latex expected value symbol - expectation
- Latex euro symbol
- Latex espace horizontal: qquad,hspace, thinspace,enspace
- Latex ensemble vide
- Latex empty set
- Latex écrire du texte dans les équations ou en mode mathématique
- Latex dérivée, limite, somme, produit et intégrale
- LateX Derivatives, Limits, Sums, Products and Integrals
- Latex degree symbol
- Latex dagger symbol or dual symbol
- Latex copyright, trademark, registered symbols
- Latex convolution symbol
- Latex congruent symbol
- Latex complex numbers
- Latex complement symbol
- Latex comment insérer une page blanche,vide avec ou sans numéro, \thispagestyle,\newpage,\usepackage{afterpage}
- Latex comment faire un underscore
- Latex ceiling function
- Latex bra ket notation
- Latex binomial coefficient
- Latex barrer du texte ou une équation
- Latex backslash symbol
- Latex arrows
- Latex accolades horizontales et verticales: \left\{,\right\},\underbrace{} et \overbrace{}
- Latex absolute value
- Laplace Transform in LaTeX
- $L^1$, $L^2$, $L^p$ and $L^\infty$ spaces in Latex
- Intersection and big intersection symbols in LaTeX
- How to write table in Latex ? begin{tabular}...end{tabular}
- How to write number sets N Z D Q R C with Latex: \mathbb, amsfonts and \mathbf
- How to write matrices in Latex ? matrix, pmatrix, bmatrix, vmatrix, Vmatrix
- How to write angle in latex langle, rangle, wedge, angle, measuredangle, sphericalangle
- How to write algorithm and pseudocode in Latex ?\usepackage{algorithm},\usepackage{algorithmic}
- How to write a vector in Latex ? \vec,\overrightarrow
- How to get dots in Latex \ldots,\cdots,\vdots and \ddots
- How to display formulas inside a box or frame in Latex ? \boxed
- Horizontal and vertical curly Latex braces: \left\{,\right\},\underbrace{} and \overbrace{}
- Greater Than or Similar To Symbol in LaTeX
- Fonction caractéristique en LaTeX
- Espaces $L^1$, $L^2$, $L^p$ et $L^\infty$ en Latex
- Écrire les ensembles classiques en Latex: \mathbb, amsfonts et \mathbf
- Dérivées partielles de fonctions à plusieurs variables en LaTeX
- Comment faire un tableau en Latex ? begin{tabular}...end{tabular}
- Comment encadrer des formules en Latex ? \boxed
- Comment écrire un angle en latex langle, rangle, wedge, angle, measuredangle, sphericalangle
- Comment écrire un algorithme en Latex ?\usepackage{algorithm},\usepackage{algorithmic}
- Comment écrire des vecteurs en Latex? \vec,\overrightarrow
- Latex FAQ