LateX Derivatives, Limits, Sums, Products and Integrals
How to write derivatives in LateX?
How to write sums in LateX?
How to write products in LateX?
How to write integrals in LateX?
Latex derivative
How to write LateX Derivatives ?
| Definition | Latex code | Result |
|---|---|---|
| First order derivative | f’(x) | \(f'(x)\) |
| Second order derivative | f’‘(x) | \(f''(x)\) |
| K-th order derivative | f^{(k)}(x) | \(f^{(k)}(x)\) |
| Partial firt order derivative | \frac{\partial f}{\partial x} | \(\displaystyle\frac{\partial f}{\partial x}\) |
| Partial Second order derivative | \frac{\partial^2 f}{\partial x^2} | \(\displaystyle\frac{\partial^2 f}{\partial x^2}\) |
| Partial k-th order derivative | \frac{\partial^{k} f}{\partial x^k}$$ | \(\displaystyle\frac{\partial^{k} f}{\partial x^k}\) |
Latex limit
How to write LateX Limits?
| Definition | Latex code | Result |
|---|---|---|
| Limit at plus infinity | \lim_{x \to +\infty} f(x) | \(\displaystyle\lim_{x \to +\infty} f(x)\) |
| Limit at minus infinity | \lim_{x \to -\infty} f(x) | \(\displaystyle\lim_{x \to -\infty} f(x)\) |
| Limit at $\alpha$$ | \lim_{x \to \alpha} f(x) | \(\displaystyle\lim_{x \to \alpha} f(x)\) |
| Inf | \inf_{x > s}f(x) | \(\displaystyle\inf_{x > s}f(x)\) |
| Sup | \sup_{x \in \mathbb{R}}f(x) | \(\displaystyle\sup_{x \in \mathbb{R}}f(x)\) |
| Max | \max_{x \in [a,b]}f(x) | \(\displaystyle\max_{x \in [a,b]}f(x)\) |
| Min | \min_{x \in [\alpha,\beta]}f(x) | \(\displaystyle\min_{x \in [\alpha,\beta]}f(x)\) |
Latex sum
How to write LateX sums?
| Definition | Latex code | Result |
|---|---|---|
| Sum | \sum | \(\displaystyle\sum\) |
| With \limits | \sum\limits_{j=1}^k A_{\alpha_j} | \(\displaystyle\sum\limits_{j=1}^k A_{\alpha_j}\) |
| Without\limits | \sum_{j=1}^k A_{\alpha_j} | \(\displaystyle\sum_{j=1}^k A_{\alpha_j}\) |
| Sum from 1 to n | \sum_{i=1}^n\sum_{i=1}^n$$ | |
| Sum off n first integers | \sum_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}{6} | \(\displaystyle\sum_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}{6}\) |
| Double sum | \sum^k_{i=1}\sum^l_{j=1}\,q_i q_j | \(\displaystyle\sum^k_{i=1}\sum^l_{j=1}\,q_i q_j\) |
Latex product
How to write LateX Products ?
| Definition | Latex code | Result |
|---|---|---|
| Product | \prod | \(\displaystyle\prod\) |
| With \limits | \prod\limits_{j=1}^k A_{\alpha_j} | \(\displaystyle\prod\limits_{j=1}^k A_{\alpha_j}\) |
| Without \limits | \prod_{j=1}^k A_{\alpha_j} | \(\displaystyle\prod_{j=1}^k A_{\alpha_j}\) |
| Product from 1 to n | \prod_{i=1}^n | \(\displaystyle\prod_{i=1}^n\) |
| Product off n first integers | \prod_{i=1}^n i | \(\displaystyle\prod_{i=1}^n i\) |
| Double product | \prod^k_{i=1}\prod^l_{j=1}\,q_i q_j | \(\displaystyle\prod^k_{i=1}\prod^l_{j=1}\,q_i q_j\) |
Latex Integral
| Definition | Latex code | Result |
|---|---|---|
| Integral | \int | \(\displaystyle\int\) |
| Integral limits | \int_{a}^b f(x)dx | \(\displaystyle\int_{a}^b f(x)dx\) |
| Double integral | \iint | \(\displaystyle\iint\) |
| Double integral with limits | \int_{a}^b\int_{c}^d f(x,y)dxdy | \(\displaystyle\int_{a}^b\int_{c}^d f(x,y)dxdy\) |
| Double integral with dots | \idotsint | \(\displaystyle\idotsint\) |
| Triple integral | \iiint | \(\displaystyle\iiint\) |
| Quadruple integral | \iiiint | \(\displaystyle\iiiint\) |
| Contour integral | \oint | \(\displaystyle\oint\) |
Latex closed surface and volume integrals
To define such integrals, you must use wasysym package
$$\displaystyle\oiint \oiiint$$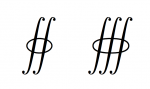
If you found this post or this website helpful and would like to support our work, please consider making a donation. Thank you!
Help UsArticles in the same category
- Variance Symbol in LaTeX
- Union and Big Union Symbol in LaTeX
- Transpose Symbol in LaTeX
- Transformée de Laplace en LaTeX
- Texte au dessus d'une flèche en LaTeX
- Text above arrow in LaTeX
- Symbole "plus grand que ou similaire à" en LaTeX
- Symbole de Variance en LaTeX
- Symbole de transposée en LaTeX
- Symbole de "non équivalent à" en LaTeX
- Symbole d'union et de grande union en LaTeX
- Symbole d'intersection et de grande intersection en LaTeX
- Strikethrough - strike out text or formula in LaTeX
- Passer en mode mathématique en Latex: $, $$ et displaymath
- Partial Derivatives of Multivariable Functions in LaTeX
- Numéroter les équations en Latex: leqno et fleqn
- Not Equivalent Symbol in LaTeX
- Latex yen symbol
- Latex valeur absolue
- Latex tensor product
- Latex symbole sous-ensemble - inclusion
- Latex symbole racine carrée
- Latex symbole produit
- Latex symbole produit vectoriel
- Latex symbole pourcentage
- Latex symbole plus ou moins
- Latex symbole parallèle
- Latex symbole orthogonal - Latex symbole perpendiculaire
- Latex symbole norme pour un vecteur ou une somme
- Latex symbole n'existe pas
- Latex symbole n'est pas un sous-ensemble - non-inclus
- Latex symbole n'est pas parallèle
- Latex symbole n'appartient pas à
- Latex symbole multiplication
- Latex symbole loi normale
- Latex symbole infini
- Latex symbole il existe
- Latex symbole il existe un seul et unique
- Latex symbole euro
- Latex symbole Est proportionnel à
- Latex symbole espérance mathématiques
- Latex symbole équivalent / équivalence
- Latex symbole dual ou dague
- Latex symbole différent
- Latex symbole dérivée partielle
- Latex symbole degré
- Latex symbole de la moyenne
- Latex symbole de la constante de Planck h
- Latex symbole congruent
- LaTeX symbole complément
- Latex symbole chapeau
- Latex symbole approximativement
- Latex symbole appartient à
- Latex symbol there exists one and only one
- Latex symbol Planck constant h
- LaTex symbol partial derivative
- Latex symbol not in
- Latex symbol not exists
- Latex symbol not equal
- Latex symbol norm for vector and sum
- Latex symbol multiply
- LaTeX symbol Is proportional to
- Latex symbol if and only if / equivalence
- Latex symbol for all x
- Latex symbol exists
- Latex symbol different
- Latex symbol checkmark
- LaTeX symbol characteristic function
- Latex symbol belongs to
- Latex symbol average
- Latex symbol approximately
- Latex subset symbol
- Latex square root symbol
- Latex real part symbol
- Latex real numbers
- Latex rational numbers
- Latex quaternion numbers
- Latex produit tensoriel
- Latex product symbol
- Latex pour tout x
- Latex points de suspension: \ldots,\cdots,\vdots et \ddots
- Latex plus or minus symbol
- Latex piecewise function
- Latex partie réelle
- Latex partie imaginaire
- Latex parallel symbol
- Latex overset and underset
- Latex orthogonal symbol - Latex perpendicular symbol
- Latex numbering equations
- Latex not subset symbol
- Latex not parallel symbol
- Latex normal distribution symbol
- Latex natural numbers
- Latex k parmi n - coefficient binomial
- Latex jacobian symbol
- Latex infinity symbol
- Latex indicator function
- Latex imaginary part symbol
- Latex how to write underscore
- Latex how to write text in math mode
- Latex how to write percent
- Latex how to write bar
- Latex how to write a fraction
- Latex how to insert a blank or empty page with or without numbering \thispagestyle,\newpage,\usepackage{afterpage}
- Latex how to hide page number
- Latex horizontal space: qquad,hspace, thinspace,enspace
- Latex hat symbol - wide hat symbol
- Latex gradient symbol
- Latex fonction plancher - Latex partie entière inférieure
- Latex fonction plafond - Latex partie entière supérieure
- Latex fonction indicatrice
- Latex floor function
- Latex flèche
- Latex expected value symbol - expectation
- Latex euro symbol
- Latex espace horizontal: qquad,hspace, thinspace,enspace
- Latex ensemble vide
- Latex empty set
- Latex écrire du texte dans les équations ou en mode mathématique
- Latex dérivée, limite, somme, produit et intégrale
- LateX Derivatives, Limits, Sums, Products and Integrals
- Latex degree symbol
- Latex dagger symbol or dual symbol
- Latex copyright, trademark, registered symbols
- Latex convolution symbol
- Latex congruent symbol
- Latex complex numbers
- Latex complement symbol
- Latex comment insérer une page blanche,vide avec ou sans numéro, \thispagestyle,\newpage,\usepackage{afterpage}
- Latex comment faire un underscore
- Latex ceiling function
- Latex bra ket notation
- Latex binomial coefficient
- Latex barrer du texte ou une équation
- Latex backslash symbol
- Latex arrows
- Latex accolades horizontales et verticales: \left\{,\right\},\underbrace{} et \overbrace{}
- Latex absolute value
- Laplace Transform in LaTeX
- $L^1$, $L^2$, $L^p$ and $L^\infty$ spaces in Latex
- Intersection and big intersection symbols in LaTeX
- How to write table in Latex ? begin{tabular}...end{tabular}
- How to write number sets N Z D Q R C with Latex: \mathbb, amsfonts and \mathbf
- How to write matrices in Latex ? matrix, pmatrix, bmatrix, vmatrix, Vmatrix
- How to write angle in latex langle, rangle, wedge, angle, measuredangle, sphericalangle
- How to write algorithm and pseudocode in Latex ?\usepackage{algorithm},\usepackage{algorithmic}
- How to write a vector in Latex ? \vec,\overrightarrow
- How to get dots in Latex \ldots,\cdots,\vdots and \ddots
- How to display formulas inside a box or frame in Latex ? \boxed
- Horizontal and vertical curly Latex braces: \left\{,\right\},\underbrace{} and \overbrace{}
- Greater Than or Similar To Symbol in LaTeX
- Fonction caractéristique en LaTeX
- Espaces $L^1$, $L^2$, $L^p$ et $L^\infty$ en Latex
- Écrire les ensembles classiques en Latex: \mathbb, amsfonts et \mathbf
- Dérivées partielles de fonctions à plusieurs variables en LaTeX
- Comment faire un tableau en Latex ? begin{tabular}...end{tabular}
- Comment encadrer des formules en Latex ? \boxed
- Comment écrire un angle en latex langle, rangle, wedge, angle, measuredangle, sphericalangle
- Comment écrire un algorithme en Latex ?\usepackage{algorithm},\usepackage{algorithmic}
- Comment écrire des vecteurs en Latex? \vec,\overrightarrow
- Latex FAQ